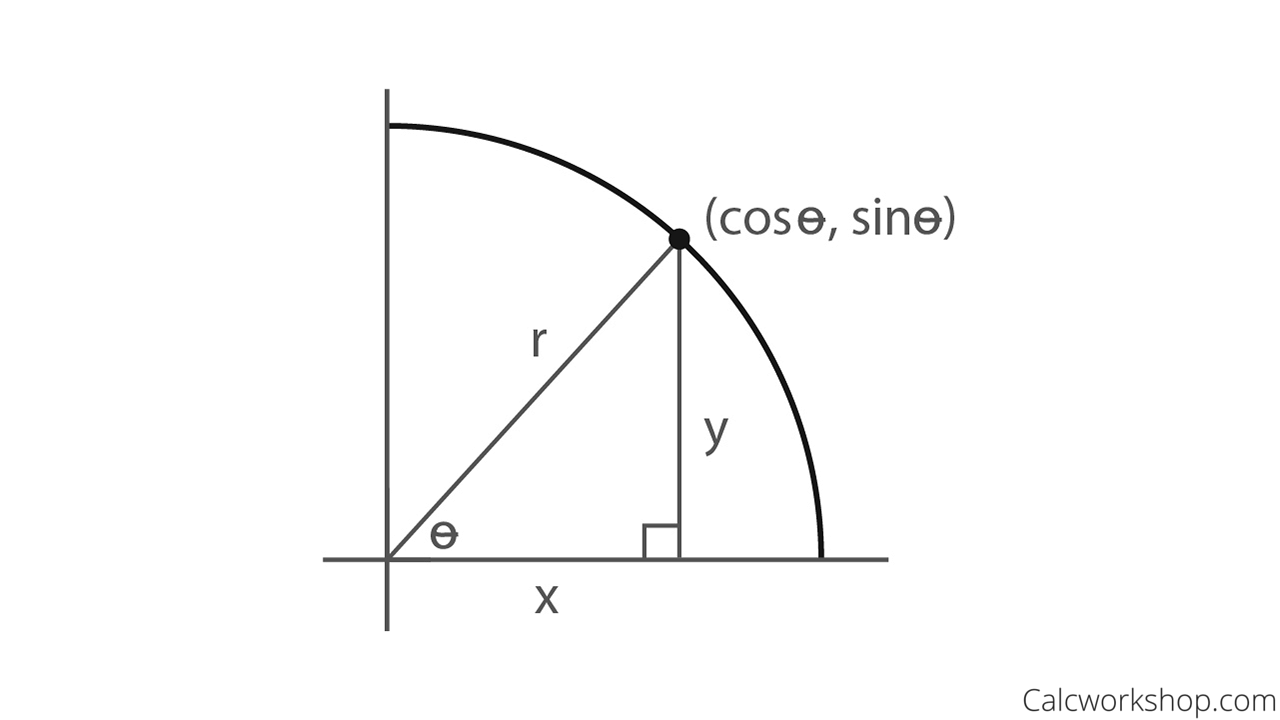Unit Circle Chart Tangent
Where t x m denotes the tangent space to m at the point x.
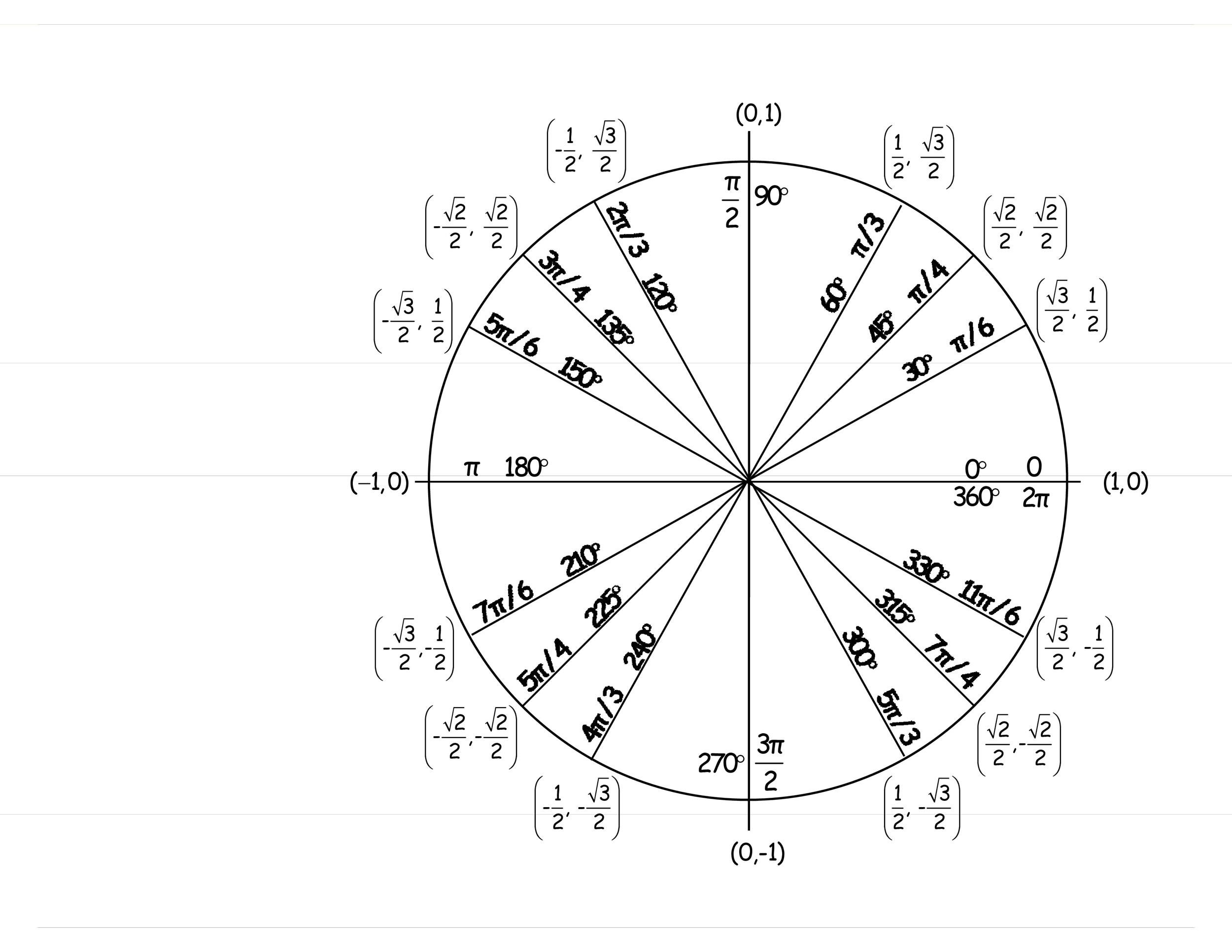
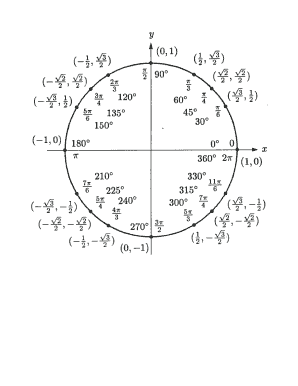
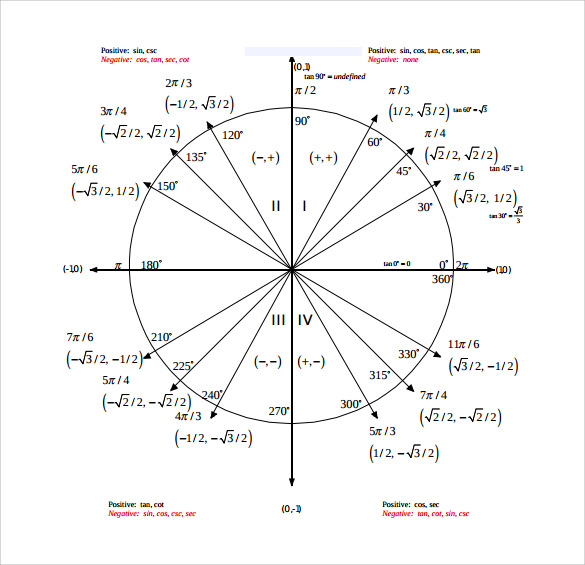
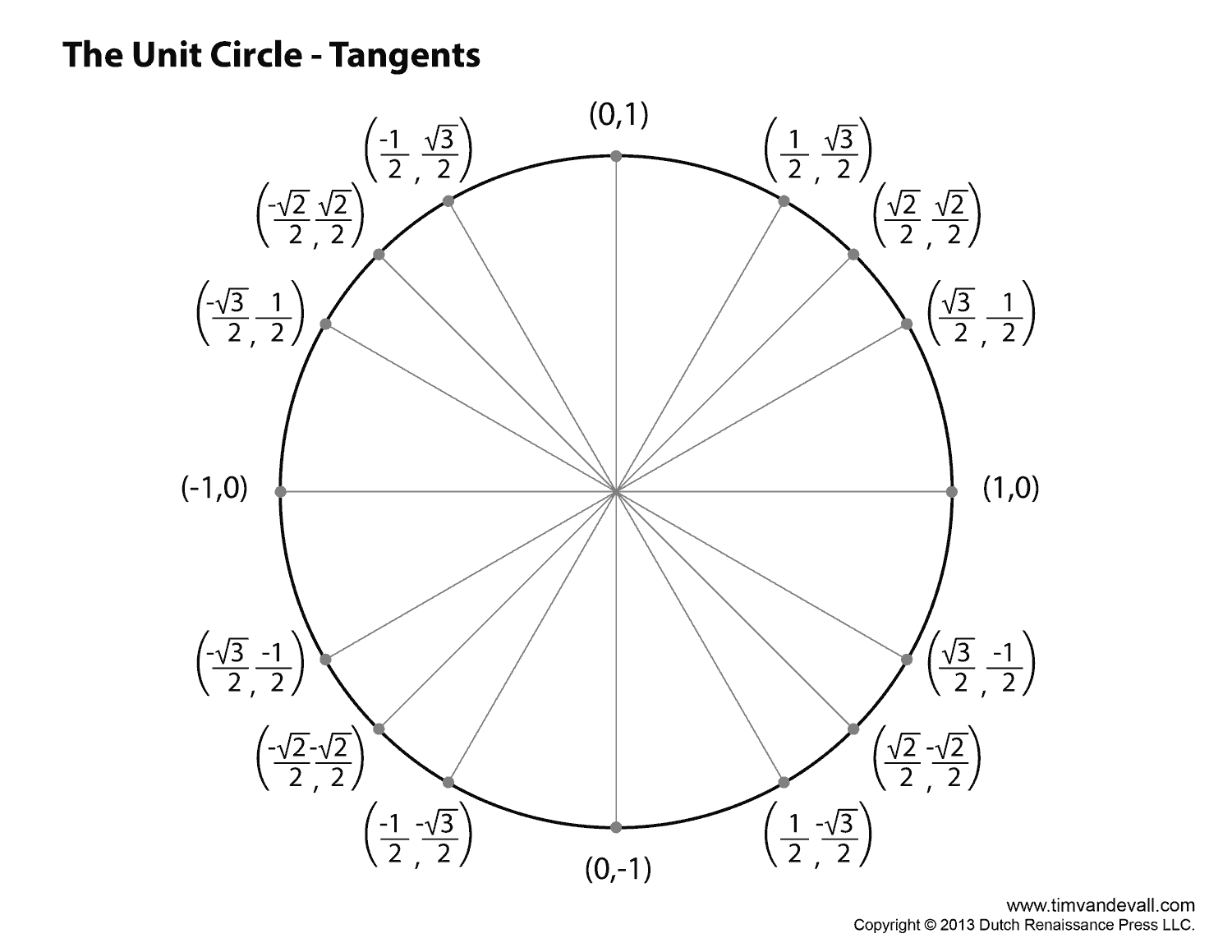
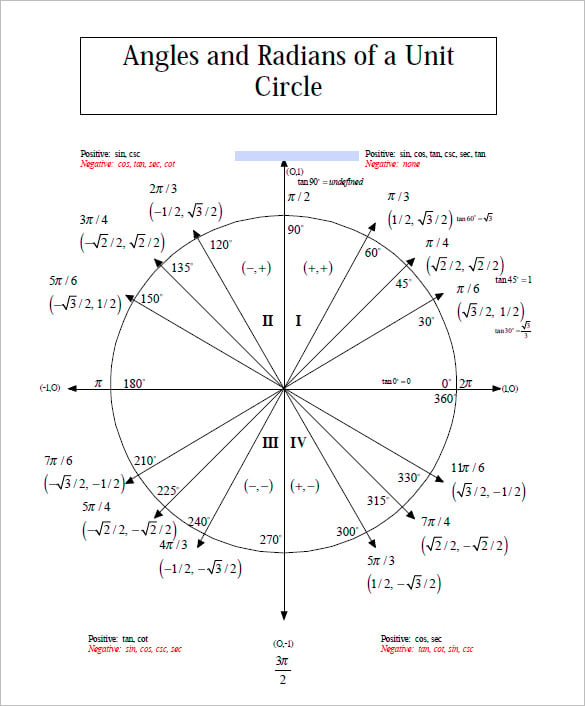
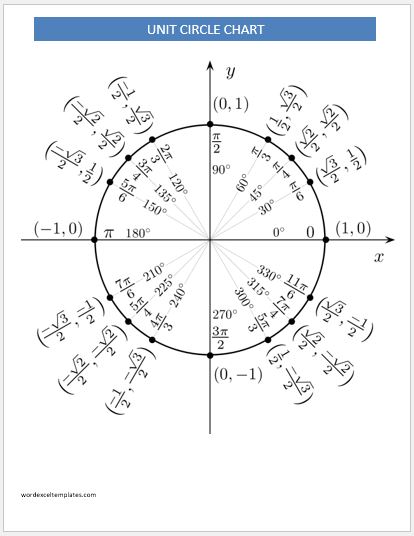
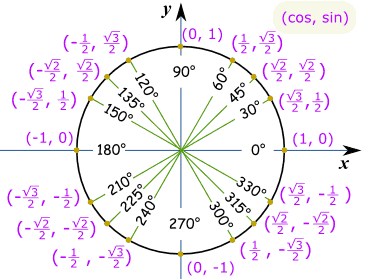
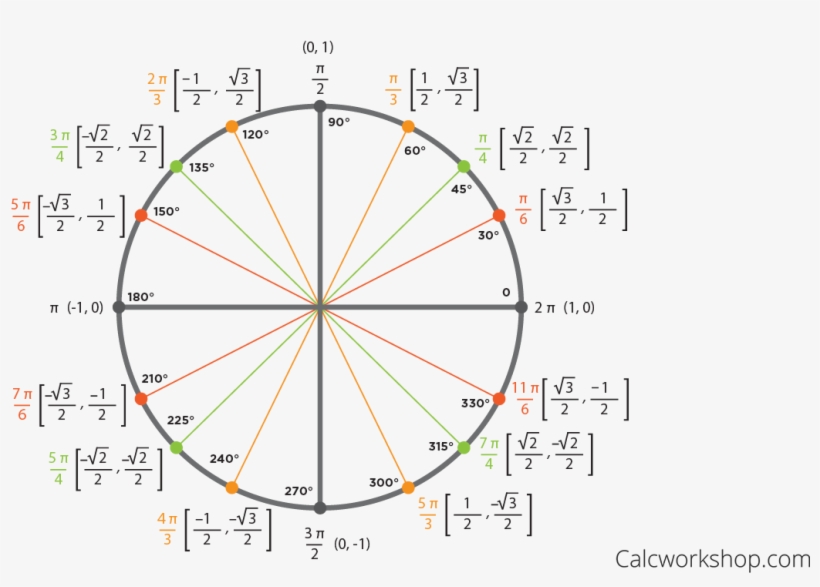
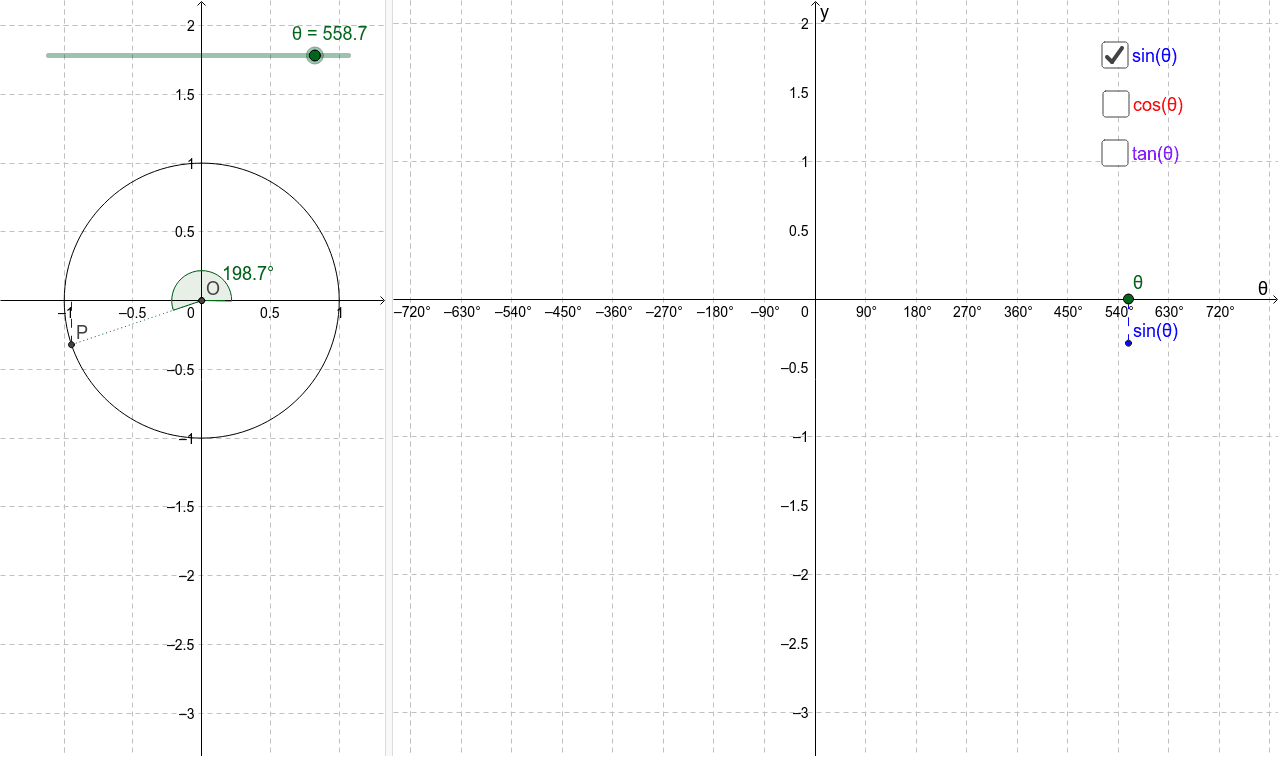
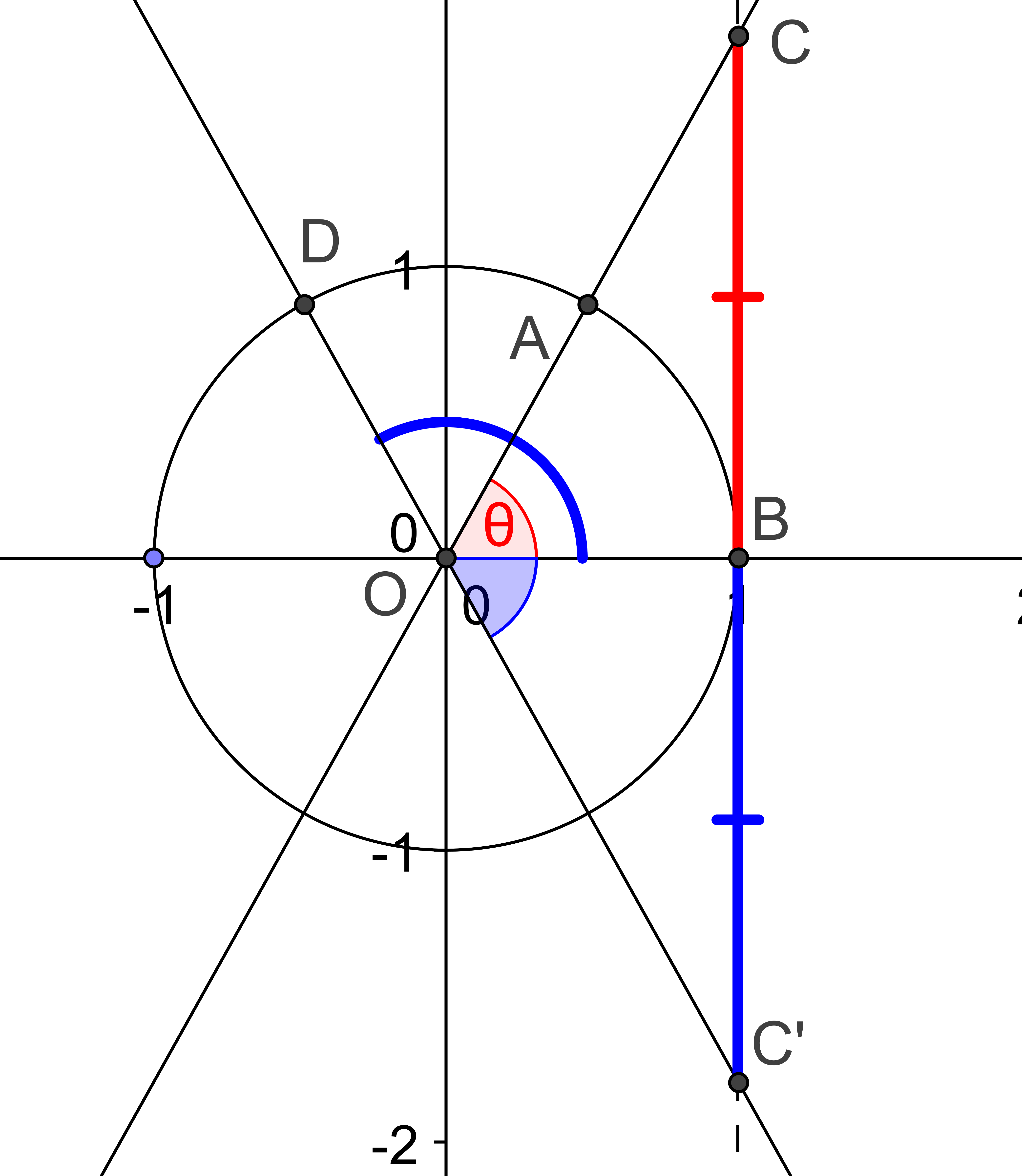
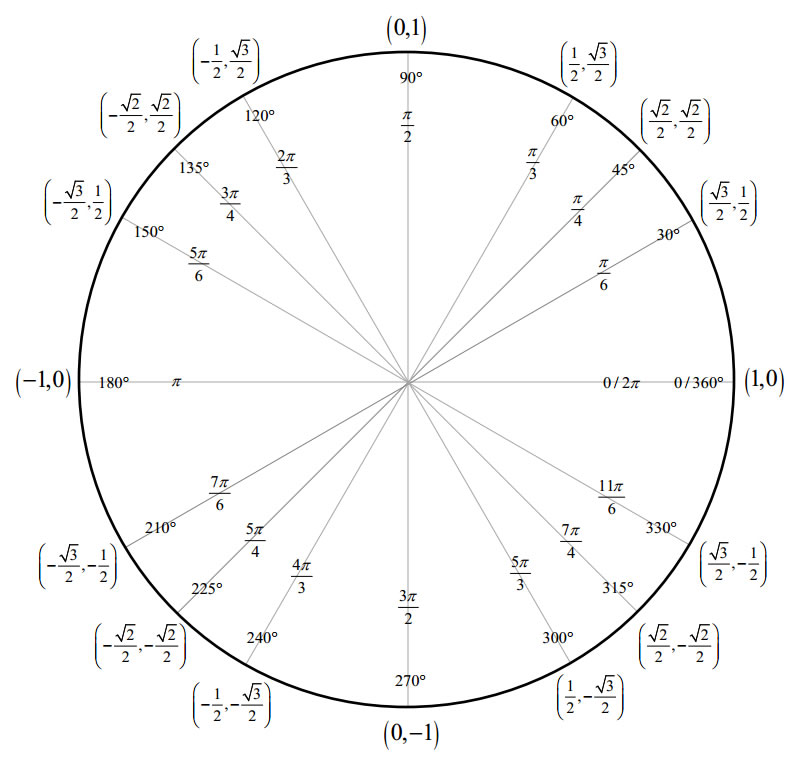
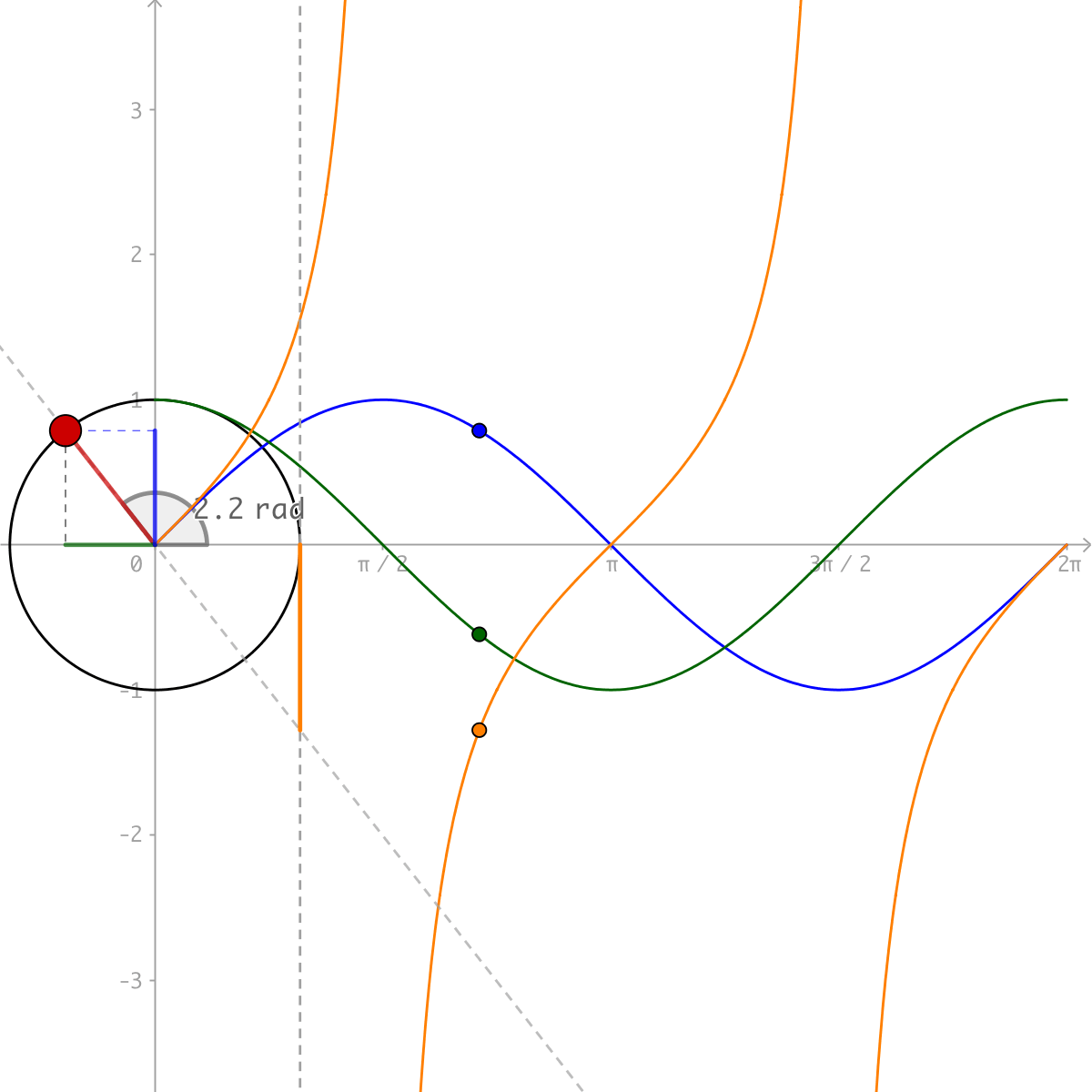
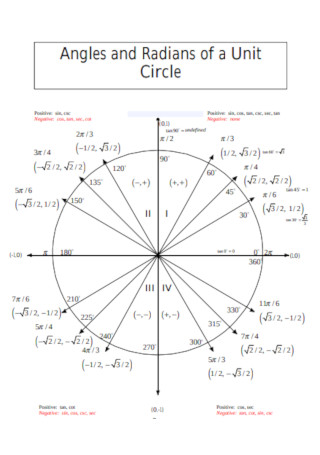
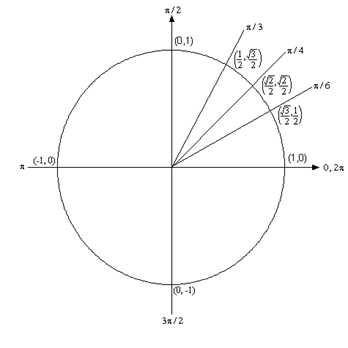
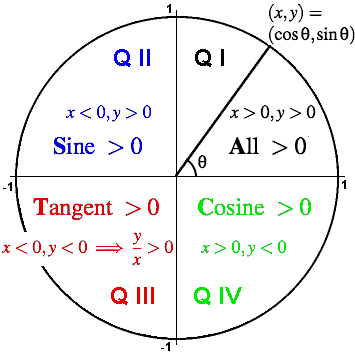
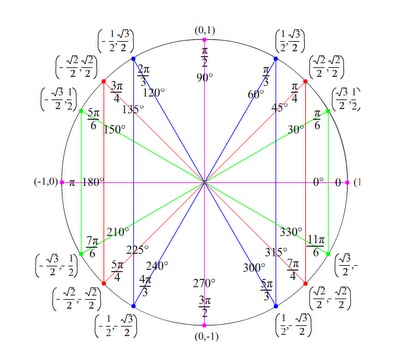
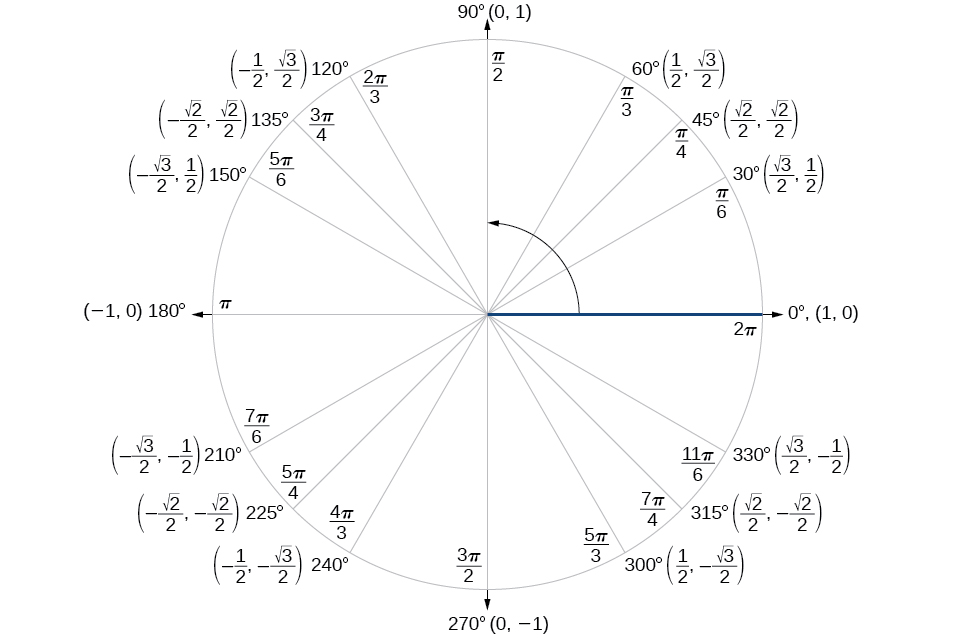
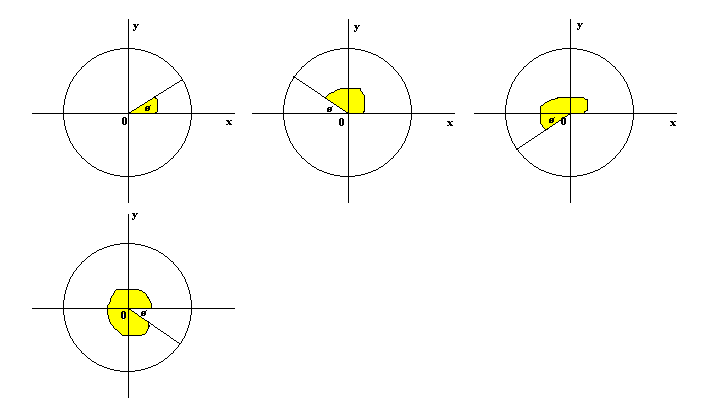
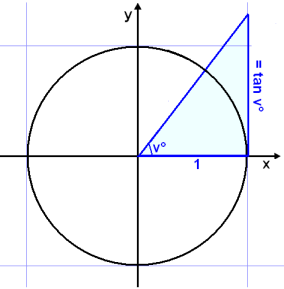
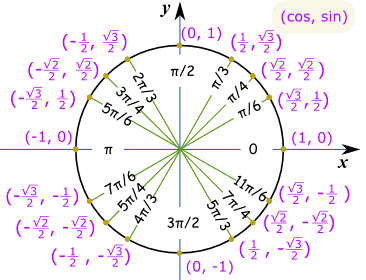
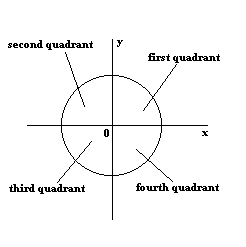
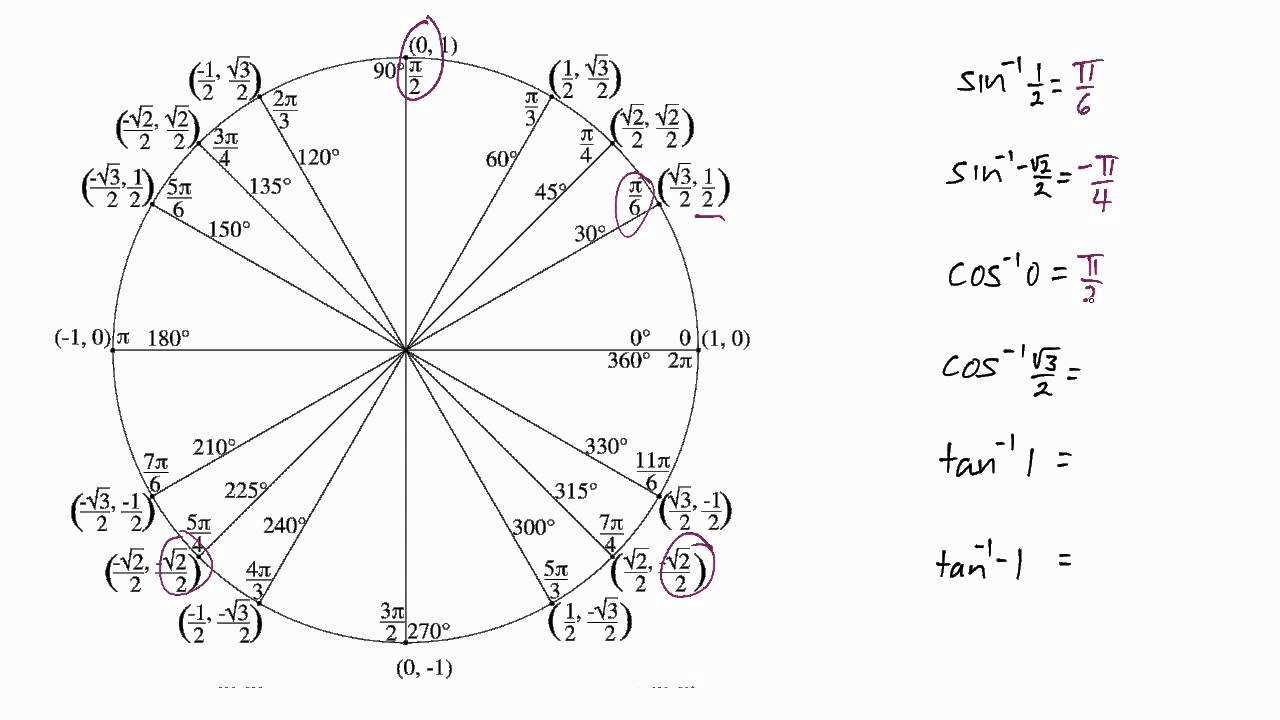
Unit circle chart tangent. It describes all the negatives and positive angles in the circle. In short it shows all the possible angles which exist. Defined by π x v x.
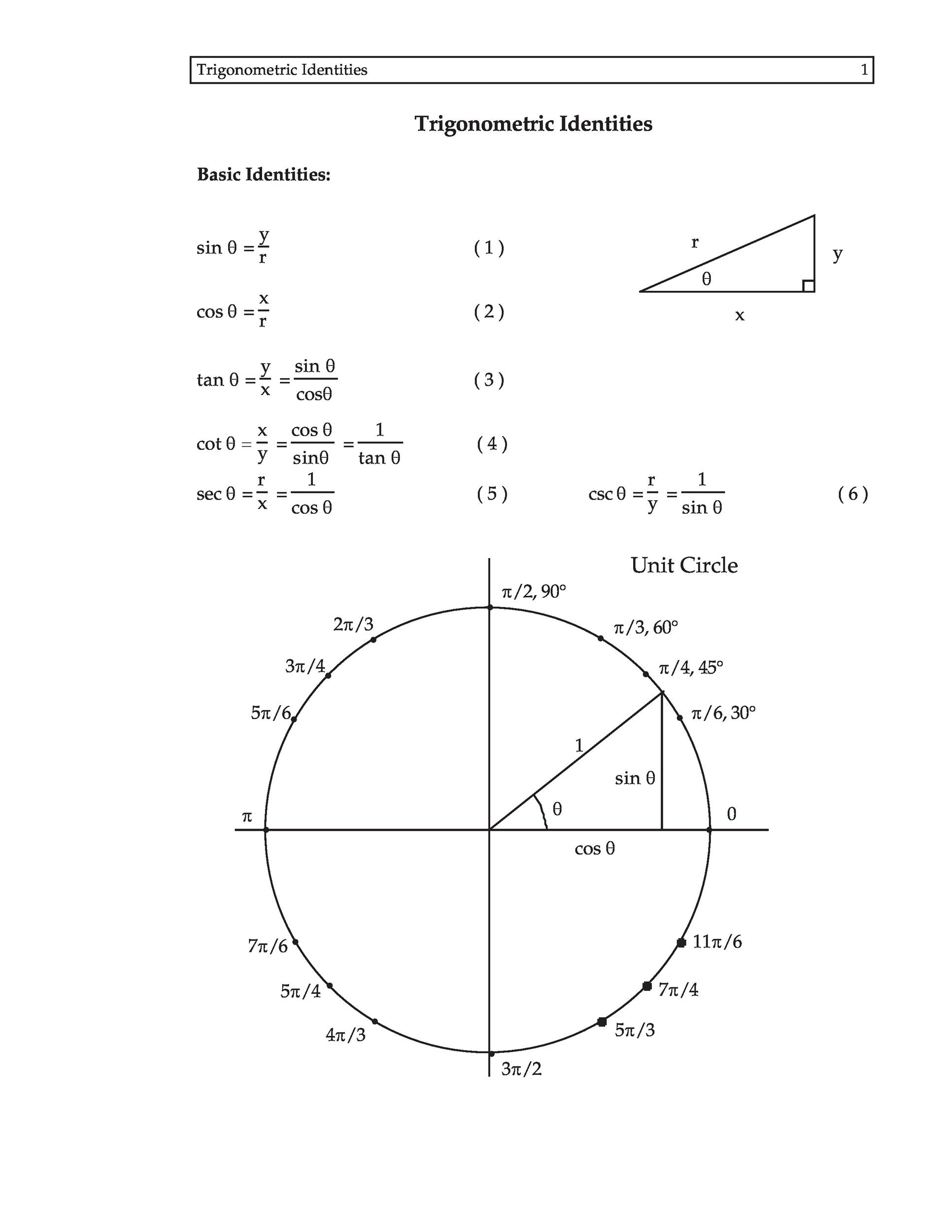
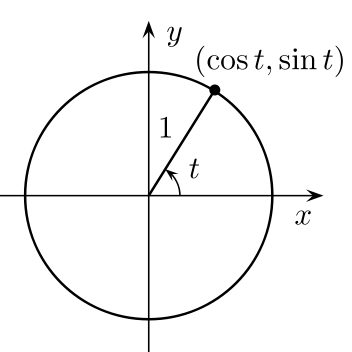
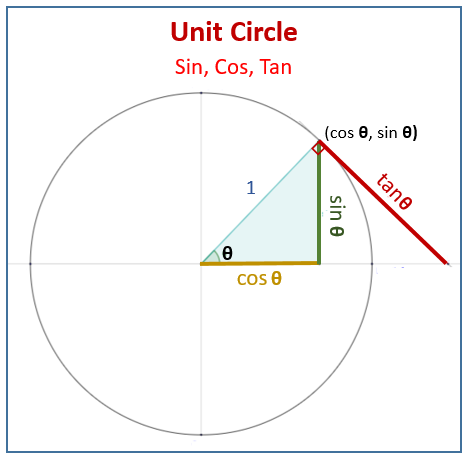
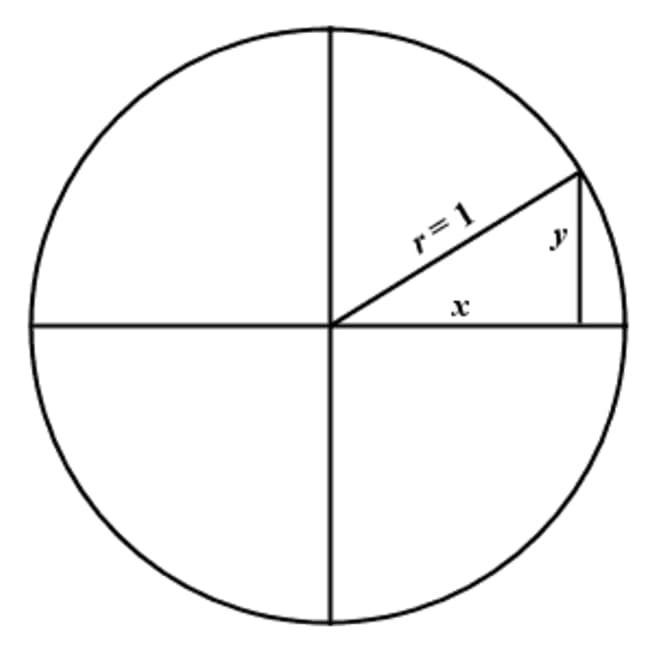
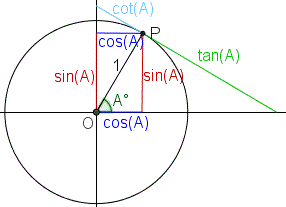
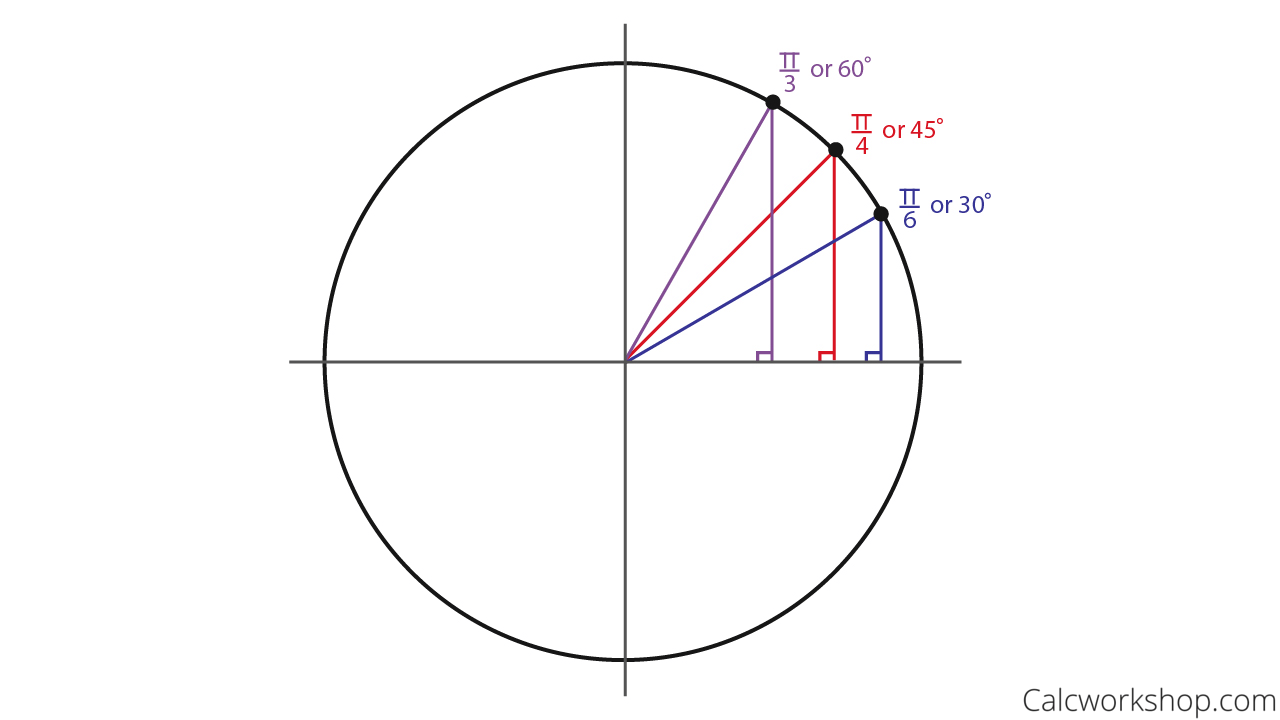
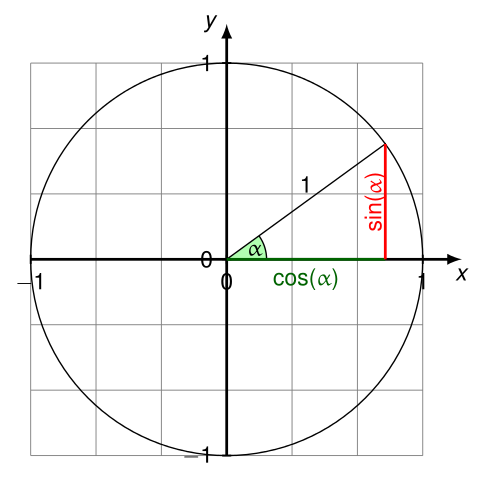
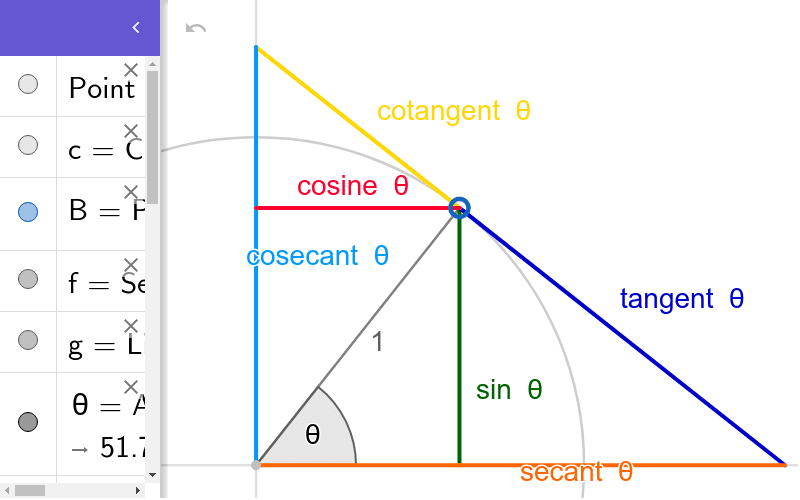
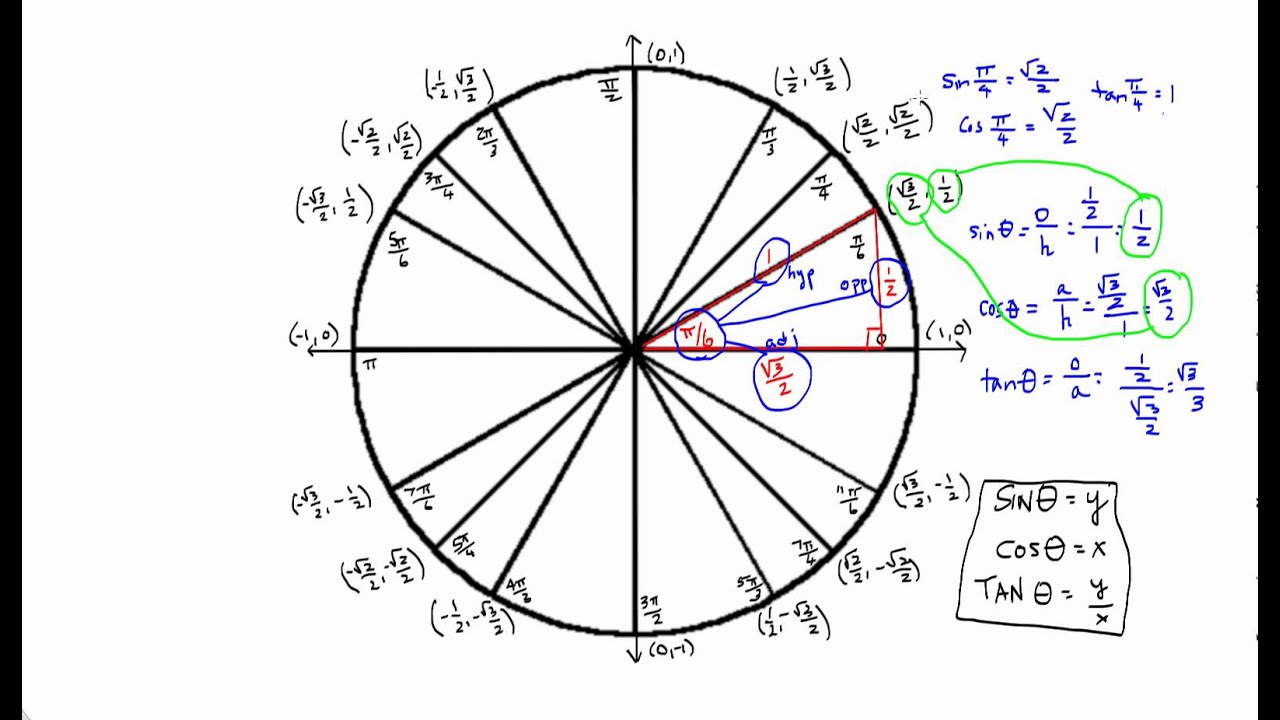
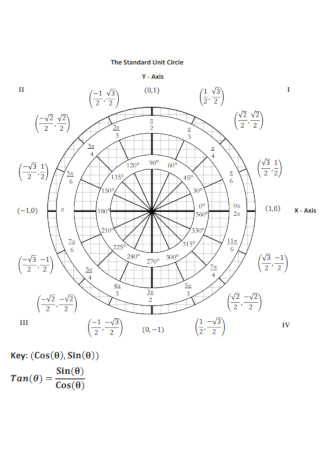
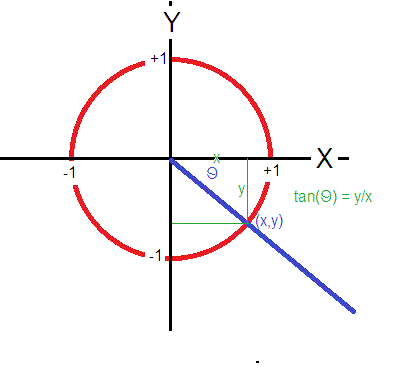
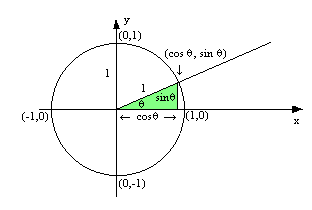
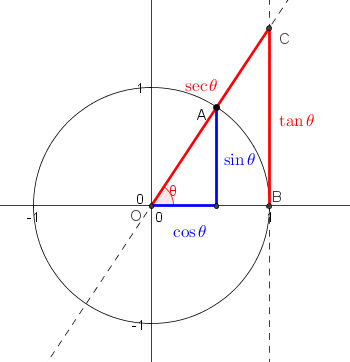
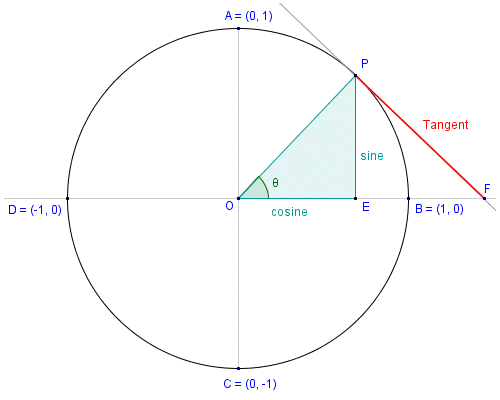
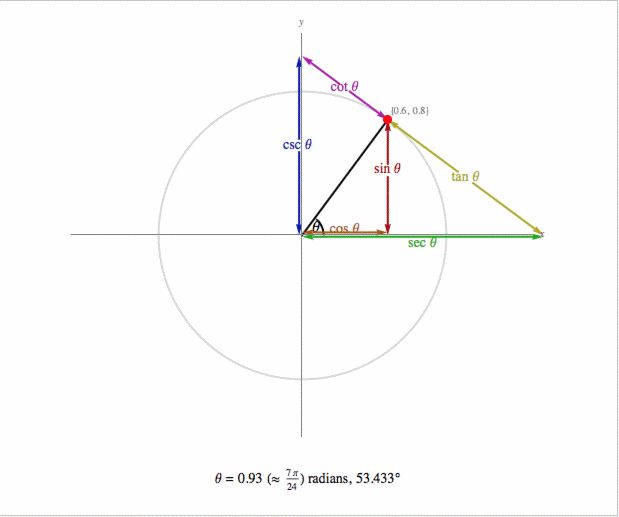
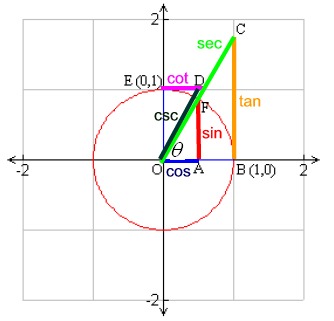
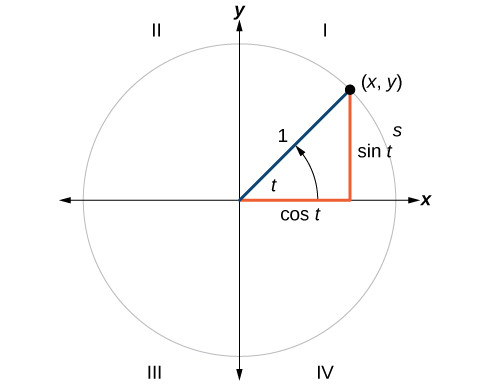
The simplest way to understand the tangent function is to use the unit circle. The x coordinate of the point where the other side of the angle intersects the circle is cos θ and the y coordinate is sin. You can use it to explain all possible measures of angles from 0 degrees to 360 degrees.
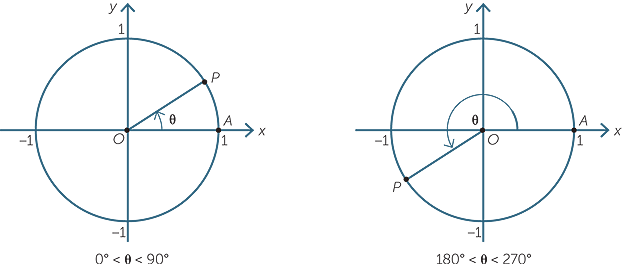
This projection maps each tangent space t x m to the single point x. To plot the parent graph of a tangent function f x tan x where x represents the angle in radians you start out by finding the vertical asymptotes. For a given angle measure θ draw a unit circle on the coordinate plane and draw the angle centered at the origin with one side as the positive x axis.
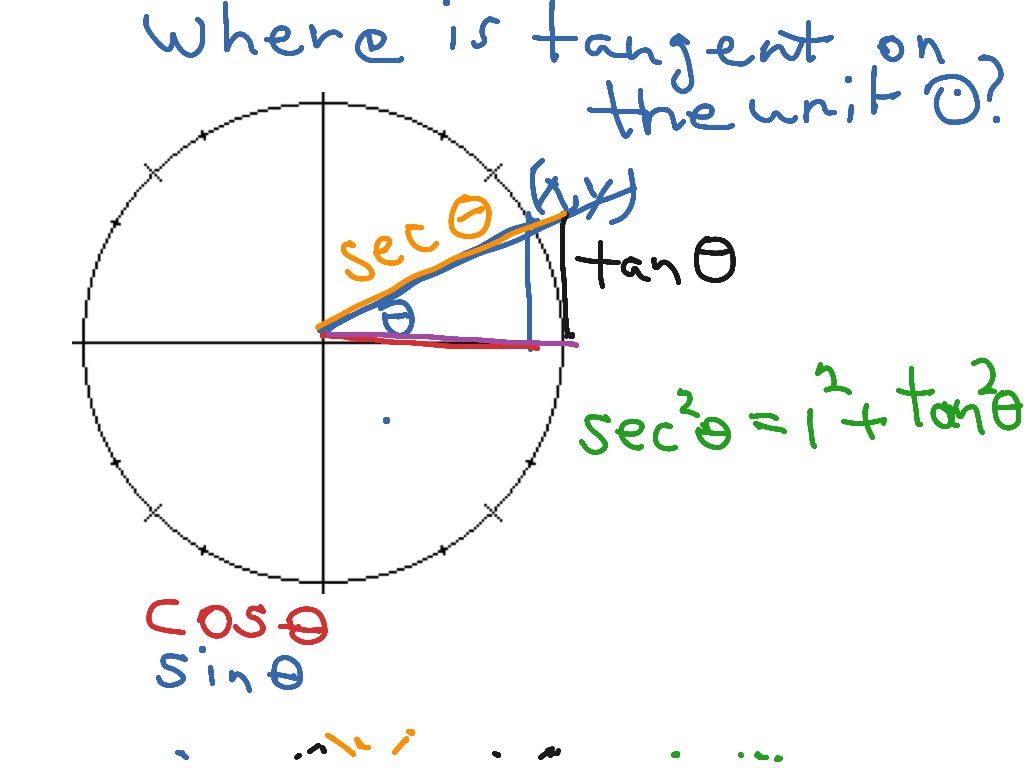
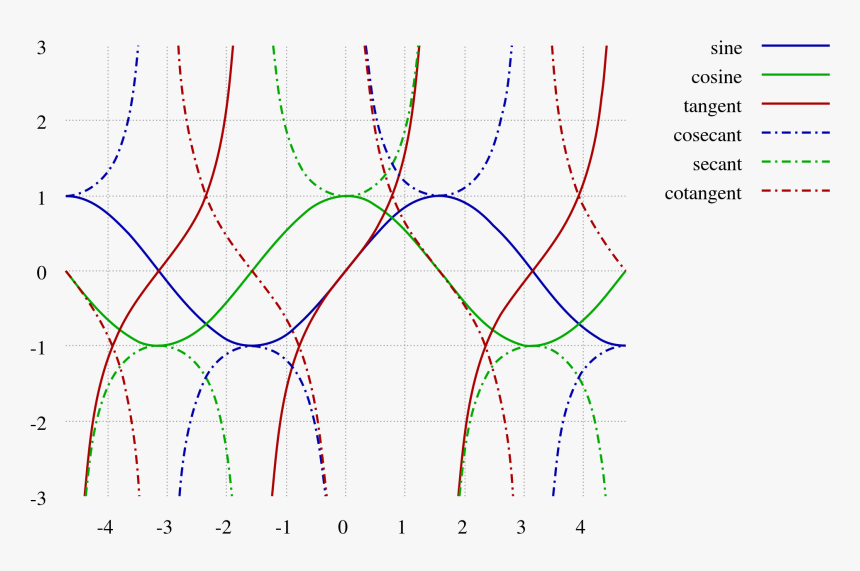
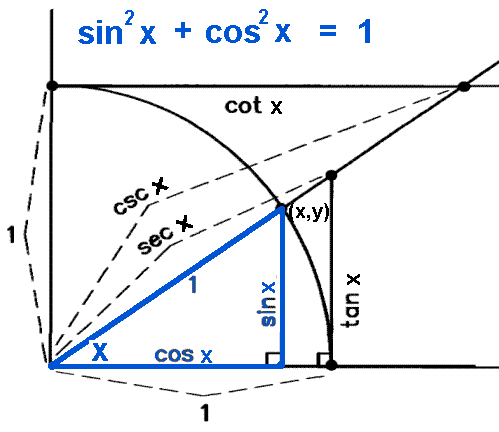
The tangent function is a periodic function which is very important in trigonometry. As you can see with this equation the tangent of an angle is equal to the y coordinate divided by the x. So an element of tm can be thought of as a pair x v where x is a point in m and v is a tangent vector to m at x.
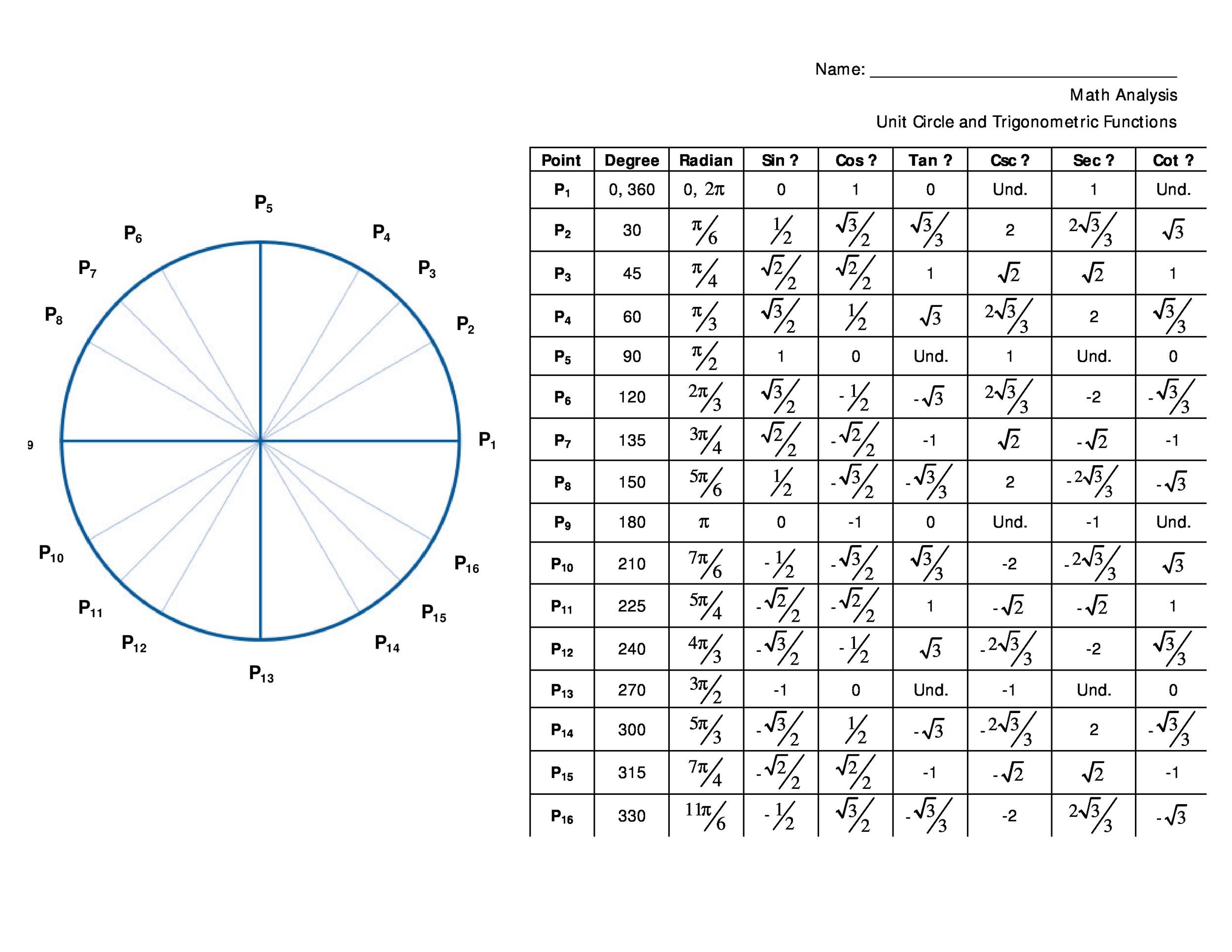
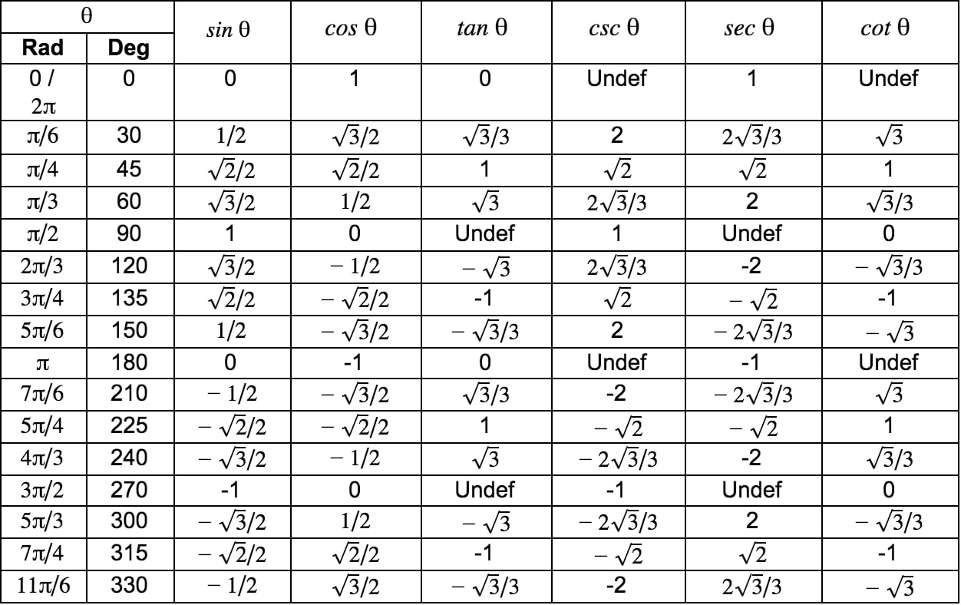
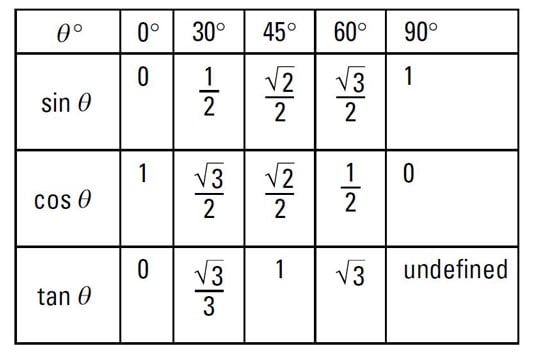
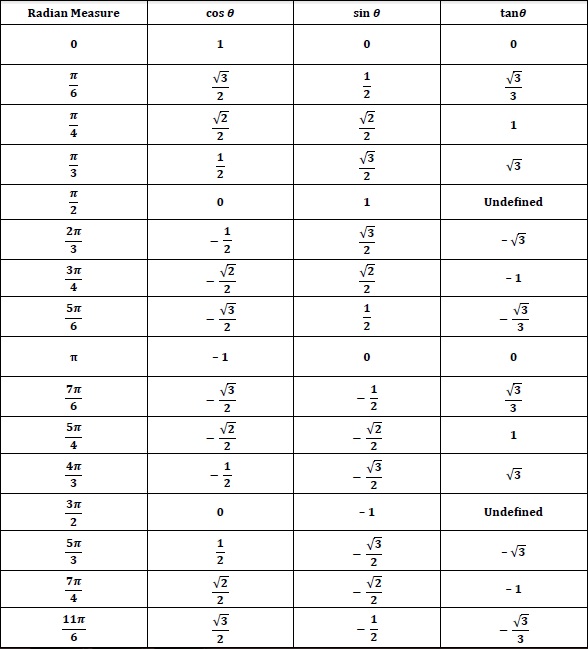
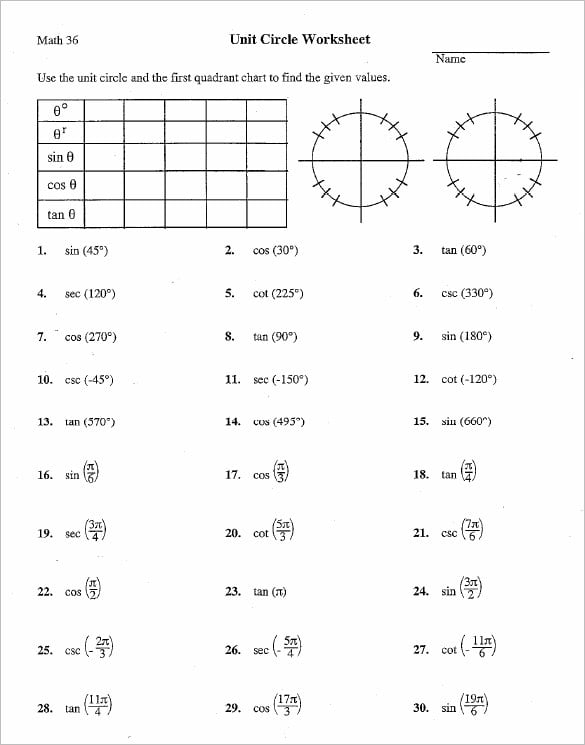
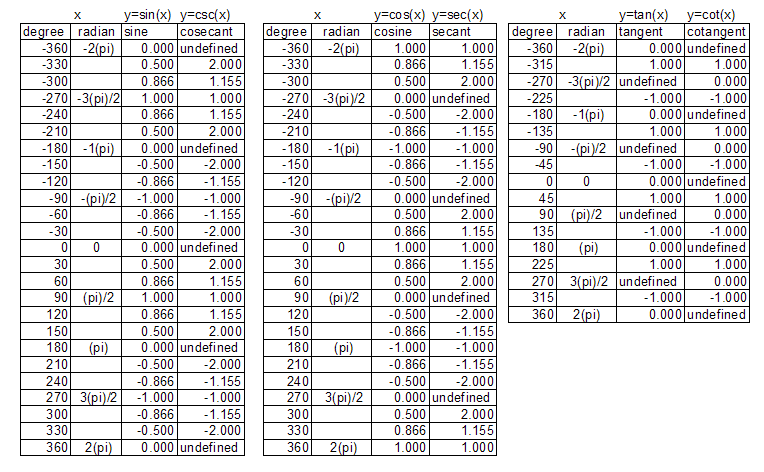
It shows the roots or zeros the asymptotes where the function is undefined and the behavior of the graph in between certain key points on the unit circle. The unit circle table of values function degree cos sin tan sec csc cot 0 1 0 0 1 undefined undefined 30 2 3 2 1 3 3 3 2 3 2 3 45 2 2 2 2 1 2 2 1 60.